I spend quite a lot of my time in meetings of various committees, sometimes acting as Chair. So, it is perhaps not surprising that I was interested to read a recent New Scientist article (“The curse of the committee”, Issue 2690, 10 January 2009) describing some recent work by a couple of Austrian physicists which set out to create a mathematical model of the interactions that occur in committees and organisations of various sizes. This work revisits ground covered in the 1950s by C Northcote Parkinson (who is one of those “famous” people belonging to my “I know the name but I don’t know why” category). Parkinson is best known for the so-called “Parkinson’s Law” which basically states that work expands to fill the time available for its completion (a principle that certainly seems to have a lot of truth in it). Anyway, the new research explored how the size of a committee or administrative structure influences its effectiveness.
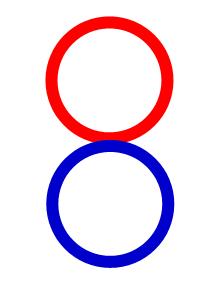
Based on knowledge of organisations throughout history, Parkinson argued that there was an upper limit on membership size beyond which an organisation becomes ineffective and will split into smaller units. The new research supports Parkinson’s hunch but more intriguingly, it was found that when the number of decision-makers involved in a group decision-making activity is eight there is a very high probability of deadlock occuring with the group splitting into two equal but opposing factions. So, the number eight is simply a bad number for committee membership etc. Thinking about this a little, it seems to me that this is an obvious result – look at the symbol for number eight: 8. It’s made up of two small loops (two groups) that touch each other but don’t overlap; two opposing factions that are unable to reach a consensus, like this: